
Neste breve estudo, exploramos o uso do processamento paralelo em operações com matrizes, sendo aplicadas as mesmas operações simples programadas em paralelo e serialmente. Utilizaremos, para tal estudo, a linguagem de programação C acrescida das bibliotecas de funções da Silicon Graphics que permitem a programação para ambientes com mais de um processador. (caso deseje veja uma introdução mais detalhada)
Em ambos os casos estudados utilizamos como matriz de trabalho uma matriz de 512x512 termos (números de ponto flutuante de dupla prescisão) o que equivale a dois Megabytes de memória. No primeiro caso definimos uma operação com a matriz tal que só é possível paralelizar o loop interno de nosso algoritmo, no segundo caso é estudada uma operação que permite a paralelização do loop externo, permitindo uma comparação entre os dois métodos e, tambem, a comparação entre estes e a versão serial do mesmo algoritmo. Nos dois casos o loop, a ser otimizado, possui a seguinte estrutura básica:
for(I1=1;I1<Tamanho_da_Matriz;I1++)
for(I2=1;I2<Tamanho_da_Matriz;I2++)
{
<Comandos de manipulação da matriz>
}
A versão serial dos respectivos algoritmos também é estudada pois ela permite otimizações na forma de se acessar a memória, o que não aconteçe nas versões paralelizadas pois, neste caso, a for
ma como é executada a programação, visando a execução em paralelo, impossibilita tais otimizações. (Caso você tenha dúvidas a respeito do significado de termos técnicos utilize este dicionário, em Inglês)
Neste primeiro caso definimos a seguinte operação: Cada termo da matriz será calculado como sendo o produto dos termos imediatamente a "cima" e ao "lado". Veja como fica a versão serial deste algoritmo:
for(I1=1;I1<Tamanho_da_Matriz;I1++)
for(I2=1;I2<Tamanho_da_Matriz;I2++)
{
Matriz[I1][I2]=Matriz[I1-1][I2]*Matriz[I1][I2-1];
}
O algoritmo foi assim implementado de forma a percorrermos a matriz através de suas colunas, pois é assim que o C armazena matrizes na memória do computador (uma seqüência linear de endereços), e acessando as informações desta forma contribuimos com o bom desempenho do sistema de cache do computador.

O elemento marcado com uma círculo acabou de ser calculado, logo os dois elementos marcados com um quadrado podem ser calculados simultaneamente, já que ambos dependem tão somente do anterior para serem calculados (além de elementos que jamais serão alterados), é fácil notar que, se continuarmos percorrendo a matriz segundo diagonais, haverá um número cada vez maior de elementos da matriz que poderão ser executados em paralelo. Como a matriz de nosso estudo tem dimensão de 512x512 logo após as primeiras interações haverá um grande número de elementos que poderão ser calculados em paralelo. De forma a acessar os elementos da matriz como exposto acima tomaremos novas variáveis para os dois loops, sendo ambas, combinação linear das antigas, temos:
J1=I1+I2 J2=I1Para aqueles acostumados com transformações de loops tal transformação equivale a se aplicar um "loop skewing" com o "skewing factor" igual a um seguido de um "loop interchange".
Rodamos a versão paralelizada (loop interno paralelizado) do nosso programa em uma estação 4D/480VGX da Silicon Graphics (oito processadores), o gráfico a seguir ilustra os resultados obtidos. Temos no eixo X o número de processadores utilizados e no eixo Y o tempo necessário para a execução do programa, a versão serial do código é mostrada para comparação.
Há três séries de dados; a primeira representa a comparação de desempenho para apenas uma repetição do conteúdo do loop interno, as demais para dez e cem repetições. Executamos o código com repetições no loop interno para que se torne possível o "controle" do número de instruções executadas em cada passo do mesmo.
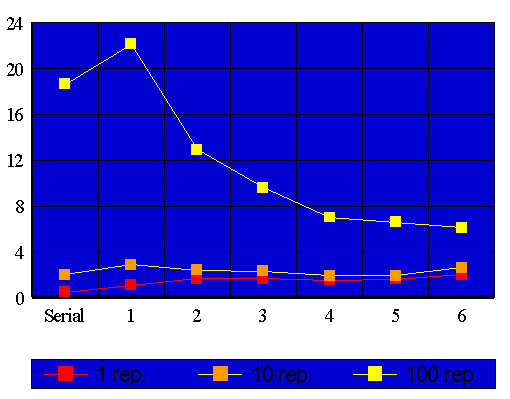
Para aqueles que não possuem um terminal gráfico ou querem consultar resultados mais detalhados criamos uma tabela.
Nota-se que, para um pequeno número de repetições a paralelização reduz a velocidade do código; já, com um número de repetições razoável, acontece o contrário. portanto, ao contrário do que a nossa primeira intuição pode levar a crer, paralelizar o código pode, em alguns casos, tornar a execução de nosso programa mais lenta.
Isto é absurdo? Nem tanto, pois o próprio trabalho de criar as divisões do programa e de computar quais termos de nossa matriz cada divisão deverá executar é uma tarefa complicada, se a tarefa final, dada a esta divisão do programa, for muito simples, não recuperaremos o tempo gasto na criação da mesma. Isto faz sentido, pois quando executamos o nosso código com cem repetições, aumentando assim o tamanho de cada "pacote" individual de instruções que podem ser executadas em paralelo, a versão paralela provou seu valor.
Outra questão intrigante: Porque a versão serial do código sempre é executada mais rapidamente do que a versão paralelizada executada em apenas um processador? Conforme dissemos anteriormente a versão serial do código foi otimizada, sempre que possível, no sentido de contribuir com o desempenho do sistema de memória do computador (Cache/RAM), ou seja foi programada de forma a minimizar o tempo que o processador espera por informações vindas da memória, maximizando assim o tempo de execução no qual o processador está efetivamente calculando o que a ele foi pedido. Já, na versão paralelizada, o código foi feito de forma a eliminar as dependências de dados entre as execuções do loop interno, acessando a memória em posições que não interferem no calculo das demais; como vimos anteriormente isto equivale a acessar a matriz segundo diagonais, que não estão armazenadas em endereços contíguos na memória, como os endereços acessados não são próximos isto dificulta o trabalho do sistema de Cache do computador, tornando o acesso a memória mais lento, portanto aumentando o tempo que o processador espera por instruções vindas da memória, ou seja, o tempo que o processador gasta para calcular as posições é, nas duas versões, praticamente o mesmo; mas na segunda versão do código o processador fica mais tempo ocioso, resultando em um desempenho total pior. Utilizando termos mais técnicos dizemos que a primeira versão do programa possui uma melhor localidade de referências do que a segunda.
Há ainda mais uma observação a ser feita. Embora fosse possível, e o mais natural, dar a cada "processador" (processo paralelo) um, e apenas um, dos "pacotes" de instruções (uma iteração do loop interno), não foi assim que fizemos. Optamos por dar a cada processador bloco maior, contendo dez "pacotes" de instruções passíveis de serem executadas em paralelo, (tamanho de bloco, na tabela) isto pode parecer estranho: Porque dar a um único processador instruções que poderiam ser executadas por dez, simultaneamente? Novamente o tempo gasto no cálculo de que "pacote de instruções" dar a cada processador entra em jogo; atribuir dez ou um "pacote" a um processador requer, praticamente, o mesmo trabalho, portanto é conveniente passar mais de um "pacote" a cada processador de forma a minimizar o tempo gasto na divisão do trabalho.
Porque não, então, dividir todo o trabalho de uma vez em blocos de tamanho igual ao numero de instruções dividido pelo número de processadores de forma que cada processador receba um grande bloco contendo um número constante de iterações? Se todas as iterações fossem iguais esta seria a melhor forma; porém isto nunca acontece, quer pelo fato dos elementos da matriz serem diferentes, quer pelo fato de haver outros programas em execução no computador de forma que nem todos os processadores serão acessados no mesmo instante, ou seja
nem todos os processadores terminarão o seu bloco de pacotes ao mesmo tempo de forma que todo o sistema terá que esperar o último processador terminar o seu bloco enquanto os demais esperam sem fazer nada. Por este fato não convém criar blocos muito grandes. Em suma, deve-se criar blocos grandes o suficiente para que não se gaste tempo demais na sua criação e pequenos o suficiente para que todo o sistema não tenha que esperar muito pelo término do processamento do último bloco.
Em nosso exemplo, definimos como dez o tamanho de bloco, é claro que definir o tamanho de bloco é uma tarefa complicada e atribuir um valor constante pode, nem sempre, ser a melhor opção porém definir uma função que calcule o melhor tamanho de bloco para cada situação é uma tarefa muito complexa, que foi deixada de lado em nosso exemplo ilustrativo. O valor dez foi fixado após testes com diversos outros valores. Outra forma interessante de se dividir o trabalho que foi executada é a passagem de novos blocos de instruções para aquelas divisões que acabaram de terminar a sua última tarefa, enquanto ainda há tarefas a serem feitas, esta é a chamada alocação dinâmica de trabalho.
Como segundo caso, definimos uma outra operação com a matriz: Cada termo da matriz será calculado como sendo o produto entre termo a cima e a esquerda (diagonalmente) e ele mesmo, a versão serial deste algoritmo é apresentada abaixo:
for(I1=1;I1<Tamanho_da_Matriz;I1++)
for(I2=1;I2<Tamanho_da_Matriz;I2++)
{
Matriz[I1][I2]=Matriz[I1-1][I2-1]*Matriz[I1][I2];
}
Novamente a versão serial do algoritmo foi implementada de forma a percorrermos a matriz através de suas colunas, pois é assim que o C armazena matrizes na memória do computador, e acessando as informações desta forma contribuimos com o bom desempenho do sistema de cache do computador, analogamente ao método usado no primeiro exemplo.J1=I1-I2 J2=I2Em termos mais técnicos esta transformação equivale a um "loop-skewing" do loop interno sobre o externo com "skewing-factor" igual a menos um.
Tendo executado a transformação descrita acima e, executando o loop externo em paralelo nos mesmos "moldes" usados para a execução do interno (mesmo computador, com loop interno adicionando repetições) obtivemos os resultados a seguir:
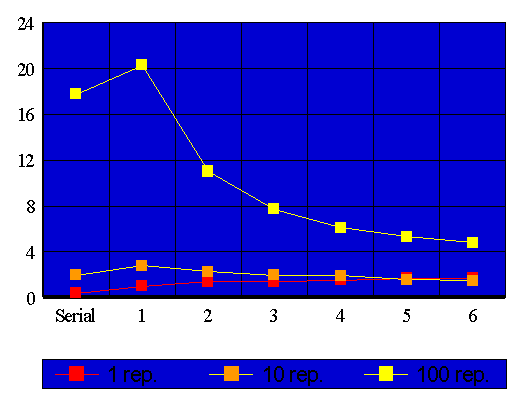
Para aqueles que não possuem um terminal gráfico ou querem consultar resultados mais detalhados criamos outra tabela.
Novamente pudemos verificar as conclusões obtidas no primeiro exemplo quanto às vantagens a respeito do acesso à memória (melhor localidade de referências da versão serial, melhorando o desempenho do sistema de memória do computador).
Neste exemplo utilizamos um "tamanho de bloco", definido similarmente na parte de paralelização do loop interno com a diferença que agora cada bloco será formado com conjuntos de iterações do loop externo; que contém, portanto, um número maior de instruções, já que uma iteraçã do loop externo equivale a um conjunto completo de iterações do loop interno, portanto cada "bloco" de instruções que será processado em paralelo é maior, ou então que, neste exemplo, tratamos de um paralelismo com granularidade mais espessa em comparação com o exemplo anterior onde tínhamos uma granularidade fina, termos estes, equivalentes aos ingleses "coarse grain parallelism" e "fine grain parallelism", definem o quão grande são os blocos de instruções a serem executados em paralelo.
Novamente foi conveniente agrupar iterações passíveis de serem executadas em paralelo, chegamos, neste exemplo a um número de cinco iterações por bloco.
De forma a tornar possível a comparaçã entre os dois tipos de paralelismo definimos duas funções: A função "Speed-Up" (ganho de velocidade), que mede o aumento na velocidade de execução do código obtido com o paralelismo em comparação com a velocidade obtida na execução serial; e a função "Custo", que mede o quanto cada processador contribui com um dado "Speed-Up", ou seja, a função "Custo" nada mais é do que a função "Speed-Up" dividida pelo número de processadores utilizados para obter o dado "Speed-Up".
apresentamos, a seguir, os gráficos de ambas as funções em ambos os casos estudados.
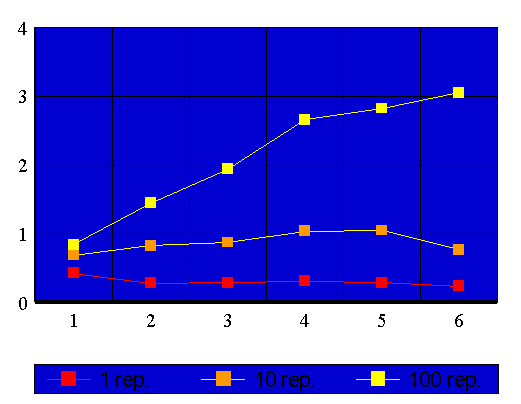
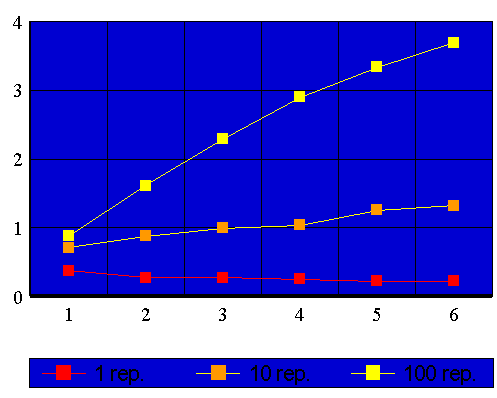
Pode-se notar que a paralelização do loop externo foi a que produziu os melhores resultados em termos de "Speed-Up", para cem repetições o ganho obtido foi maior e para dez repetições obteve-se algum ganho com a paralelização do loop externo em contrapartida com o ganho (máximo) praticamente igual a um no caso da paralelização do loop interno; no caso de uma repetição é fácil notar a ineficiência da programação em paralelo.
Já é possível, com os dados que dispomos, chegar a outra conclusão importante: O paralelismo de grão fino &etilde; menos eficiente do que o paralelismo de grão espesso; esta é, segundo pesquisas mais detalhadas, uma regra geral, não apenas válida para o nosso exemplo de estudo mas para todo o tipo de programa a ser executado em paralelo. Portanto, se você pretende obter um bom ganho de velocidade, concentre seus esforços no sentido de paralelizar os loops mais externos do seu programa, de forma a obter um código paralelo com a granularidade mais espessa possível.
Tal fato pode ser explicado se pensarmos que, quando se paraleliza o loop externo, a criação de divisões do programa é feita apenas uma vez, já que o loop mais externo é o que será paralelizado. No caso da paralelização do loop interno, a cada nova iteração do loop externo as divisões são "acionadas" (pois elas são criadas na primeira iteração e reutilizadas nas demais), este "acionamento" não é uma tarefa trivial no sentido que será gasto um certo tempo para fazê-lo, se levarmos em conta que, no nosso exemplo, este reacionamento ocorre mais de mil vezes é razoável se pensar que esta paralelização não é tão eficiente quanto a paralelização do loop externo, onde a criação de divisões acontece apenas uma vez. Convém ressaltar que, para qualquer tipo de dependência de dados (do tipo acesso a matrizes, bastante comum) é possível paralelizar o(s) loop(s) interno(s), já a paralelização do loop externo requer condições muito mais específicas. É claro que a possibilidade de paralelizar não implica em um necessário ganho de velocidade, como pode ser visto nos exemplos acima.
Outro ponto importante a ser ressaltado é que, em um sistema multi-processado, a utilização de mais processadores não leva sempre a um aumento de velocidade, ao contrário do que os nossos gráficos de Speed-Up levam a crer, pois a adição de mais um processador implica, durante a execução, em um gasto adicional de tempo para criar mais uma divisão do programa para o novo processador; como a quantidade de trabalho é a mesma, sendo dividida entre um maior número de processadores, se continuarmos a colocar um maior número de processadores chegará um instante que a adição de mais um processador prejudicará o desempenho, no sentido que será gasto um tempo para criar a divisão relativa àquele processador e o trabalho, por ele executado, será pequeno demais para compensar o tempo perdido durante a criação da sua divisão.
Além disto os processadores são dispositivos eletrônicos de custo elevado. Deve-se, portanto, avaliar a relação custo benefício, na utilização de mais processadores para executar uma mesma tarefa, com este intuito apresentamos, a seguir, os gráficos da função custo:
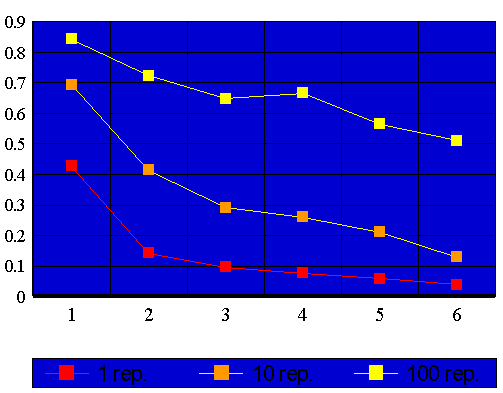
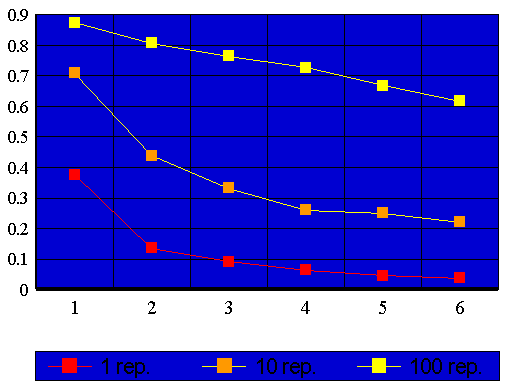
Pode-se notar nos gráficos acima que a inclusão de mais um processador não aumenta a velocidade do código em uma proporção linear, cada processador adicionado aumenta a velocidade do sistema (neste caso, antes do limite crítico exposto acima) porém cada novo processador contribui com um aumento relativo cada vez menor. Tendo-se em vista o custo efetivo de cada processador, o programador deve optar por utilizar um número de processadores menor do que aquele que fornece o desempenho máximo. Podemos estabelecer um critério como o seguinte: quando o aumento de velocidade propiciado pelo acréscimo de um processador atingir um nível pré definido, definir aquele número de processadores como ideal, devido à relação custo benefício. Por exemplo, se chegarmos a conclusão que: Dado o custo da utilização de mais um processador e o ganho de velocidade propiciado, por este processador, em uma dada aplicação, é conveniente utilizar mais processadores até que o "Speed-Up" relativo à adição daquele processador atinja, ultrapassando ou não, o valor 0,7. Se este fosse o valor ideal para a aplição similar a nossos exemplos deveríamos executar o primeiro programa com três processadores e o segundo com cinco.
Apresentamos, a seguir, as nossas conclusões em forma de lista:
Estudante de graduação em engenharia elétrica na Escola Politécnica da USP.
Estagiário do Laboratório de Sistemas Integrados, Poli - Elétrica.
Orientador: Edson Toshimi Midorikawa.
![]() Laboratory of Integrated Systems
Laboratory of Integrated Systems
last modified: 29-aug-95